


Grundlagen und Methoden der Physiologie; molekulare und zelluläre Aspekte

 Streuung,
Normalwerte, Biometrie, Hypothesenverifizierung
Streuung,
Normalwerte, Biometrie, Hypothesenverifizierung




 Streuung,
Normalwerte, Biometrie, Hypothesenverifizierung
Streuung,
Normalwerte, Biometrie, Hypothesenverifizierung
 Bayes-Theorem: Thomas Bayes
Bayes-Theorem: Thomas Bayes| Biometrie
(Biostatistik) verwendet mathematische Verfahren zur Organisation,
Darstellung und Beurteilung von Daten, die bei der wissenschaftlichen
Untersuchung biologischer Systeme gewonnen werden. Sie stellt Ergebnisse von Beobachtungen oder experimentellen Studien dar (beschreibende oder deskriptive Statistik), bietet Schätz- und Testverfahren, und ermöglicht die Prüfung von Hypothesen (schließende oder induktive Statistik). Bei letzterer können zwei Arten von Fehleinschätzungen unterlaufen: -- Fehler 1. Art, α-Fehler: Die Nullhypothese (Gruppen unterscheiden sich nicht) wird fälschlicherweise zurückgewiesen, obwohl sie zutrifft (falsch positive Einschätzung: Ein Unterschied wird vermutet, obwohl es nicht da ist. Beispiele: Krankheitsdiagnose beim Gesunden, zu strenger Prüfer - "Fehlalarm"). Hohe Spezifität bedeutet einen geringen Fehler 1. Art -- Fehler 2. Art, β-Fehler: Die Nullhypothese wird fälschlicherweise beibehalten, obwohl sie nicht zutrifft (falsch negative Einschätzung - es wird etwas verpasst, obwohl es da ist. Beispiele: Nichterkennen einer Krankheit, allzu nachsichtiger Prüfer - "Laissez-faire"). Hohe Sensitivität bedeutet einen geringen Fehler 2. Art Das Ergebnis von Beobachtungen / Messungen unterliegt verschiedenen Fehlerquellen. Beispielsweise stellt sich die Frage nach der Genauigkeit: -- Mit Präzision meint man, wie stark (bei wiederholter Messung) die Resultate streuen (quantifizierbar mittels eines Varianzmaßes, z.B. Standardabweichung); -- Absolutgenauigkeit (accuracy) gibt an, wie "richtig" das Messverfahren arbeitet (Nähe des statistischen Mittelwertes der Resultate zum tatsächlichen Wert der gemessenen Größe). Testdesign bedeutet planvolles Vermeiden von Fehlern. So ermöglicht Randomisierung (zufällige Zuteilung zu Testgruppen), unbeabsichtigte systematische Fehler (bias) zu vermeiden, welche z.B. einen Effekt (etwa eine Medikamentenwirkung) vortäuschen, der in Wirklichkeit nicht besteht. |
 Beschreibende Statistik
Beschreibende Statistik  Absolutgenauigkeit / Präzision
Absolutgenauigkeit / Präzision  Schließende Statistik
Schließende Statistik  Fehler (α, ß), Spezifität / Sensitivität
Fehler (α, ß), Spezifität / Sensitivität  Bayes'sche Statistik
Bayes'sche Statistik  Hypothesentestung
Hypothesentestung
 Quartilsabstand
Quartilsabstand  Genauigkeit / Präzision
Genauigkeit / Präzision  Referenzbereich
Referenzbereich  Konfidenzintervall
Konfidenzintervall  Nullhypothese
Nullhypothese
 qualitativ (ohne zahlenmäßige Ordnung, z.B. jung / alt, männlich / weiblich) oder
qualitativ (ohne zahlenmäßige Ordnung, z.B. jung / alt, männlich / weiblich) oder

 quantitativ; ein quantitatives Merkmal ist
quantitativ; ein quantitatives Merkmal ist diskret (Wertebereich: natürliche
Zahlen, z.B. Leukozytenzahl) oder
diskret (Wertebereich: natürliche
Zahlen, z.B. Leukozytenzahl) oder  stetig (Wertebereich: reelle Zahlen,
d.h. auf einer kontinuierlichen Skala liegend, z.B. Betrag des
Blutdrucks).
stetig (Wertebereich: reelle Zahlen,
d.h. auf einer kontinuierlichen Skala liegend, z.B. Betrag des
Blutdrucks). 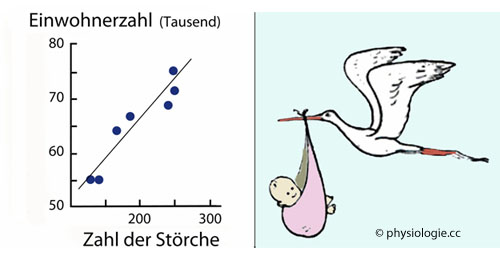
 Abbildung: Korrelation bedeutet nicht notwendigerweise Kausalität (Verursachung)
Abbildung: Korrelation bedeutet nicht notwendigerweise Kausalität (Verursachung) . Sie kann aus Zufall oder willkürlicher Auswahl von Datenpunkten resultieren, oder auf einer gemeinsamen (dahinterliegenden) Ursache beruhen, die beide Zustandsvariablen unabhängig voneinander beeinflusst
. Sie kann aus Zufall oder willkürlicher Auswahl von Datenpunkten resultieren, oder auf einer gemeinsamen (dahinterliegenden) Ursache beruhen, die beide Zustandsvariablen unabhängig voneinander beeinflusst
 Das Vorliegen einer Korrelation kann eine direkte Ursache nahelegen, muss es aber nicht ( wie in der obigen
Das Vorliegen einer Korrelation kann eine direkte Ursache nahelegen, muss es aber nicht ( wie in der obigen  Abbildung anhand eines grotesken Beispiels gezeigt - unabhängig, wie "signifikant" der Wahrscheinlichkeitswert der Korrelation ist).
Abbildung anhand eines grotesken Beispiels gezeigt - unabhängig, wie "signifikant" der Wahrscheinlichkeitswert der Korrelation ist).  Beschreibende
(deskriptive) Statistik - sie vermittelt Verfahren zur übersichtlichen
Darstellung von Untersuchungsergebnissen, wie
Mittelwert und Streumaße, z.B. die Varianz:
Beschreibende
(deskriptive) Statistik - sie vermittelt Verfahren zur übersichtlichen
Darstellung von Untersuchungsergebnissen, wie
Mittelwert und Streumaße, z.B. die Varianz:
 Diese quantifiziert, wie breit die Streuung der Einzelwerte einer
entsprechenden Größe in einer Gruppe ist (z.B. die Verteilung des
Körpergewichts der Schüler einer Klasse);
Diese quantifiziert, wie breit die Streuung der Einzelwerte einer
entsprechenden Größe in einer Gruppe ist (z.B. die Verteilung des
Körpergewichts der Schüler einer Klasse); Erkundende (explorative) Statistik - sie versucht, Daten, über deren Struktur wenig bekannt ist, sinnvoll darzustellen;
Erkundende (explorative) Statistik - sie versucht, Daten, über deren Struktur wenig bekannt ist, sinnvoll darzustellen; Schließende
(induktive) Statistik - sie bietet Schätz- und Testverfahren,
ermöglicht die Prüfung von Hypothesen durch statistische Tests.
Annahmen können bei geringer Wahrscheinlichkeit für ihre Gültigkeit als
widerlegt gelten (Falsifizierung:
Schließende
(induktive) Statistik - sie bietet Schätz- und Testverfahren,
ermöglicht die Prüfung von Hypothesen durch statistische Tests.
Annahmen können bei geringer Wahrscheinlichkeit für ihre Gültigkeit als
widerlegt gelten (Falsifizierung:
 Statt einer vorgeschlagenen Hypothese nimmt man im Fall ihrer
Widerlegung eine als besser geeignet erscheinende Antithese an).
Statt einer vorgeschlagenen Hypothese nimmt man im Fall ihrer
Widerlegung eine als besser geeignet erscheinende Antithese an).  Lokalisationsmaße: Bezüglich der "Schwerpunkte" von Verteilungen unterscheidet man Mittel-, Median- und Modalwerte (
Lokalisationsmaße: Bezüglich der "Schwerpunkte" von Verteilungen unterscheidet man Mittel-, Median- und Modalwerte ( Abbildung), um die herum die einzelnen Beobachtungswerte zu liegen kommen (s. weiter unten):
Abbildung), um die herum die einzelnen Beobachtungswerte zu liegen kommen (s. weiter unten):
 Abbildung: Mittel-, Median- und Modalwert einer Verteilung
Abbildung: Mittel-, Median- und Modalwert einer Verteilung Der Modalwert ist der am häufigsten vorkommende Wert in der
Stichprobe, der Medianwert teilt die Stichprobe in zwei gleich große
Hälften, und der (arithmetische) Mittelwert gibt den durchschnittlichen Messwert (Summe der Messwerte / Zahl der Beobachtungen) an.
Der Modalwert ist der am häufigsten vorkommende Wert in der
Stichprobe, der Medianwert teilt die Stichprobe in zwei gleich große
Hälften, und der (arithmetische) Mittelwert gibt den durchschnittlichen Messwert (Summe der Messwerte / Zahl der Beobachtungen) an.
| AMW = (E1 + E2 ... + EN) / N |
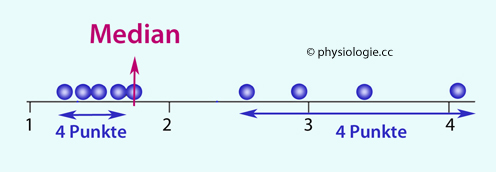
 Abbildung: Medianwert
Abbildung: Medianwert
 Dispersionsmaße: Bezüglich der Streubereiche stellt man die Häufigkeitsverteilung der Messwerte einer Gruppe von Beobachtungen (einer repräsentativen Stichprobe. sample - Teil der Grundgesamtheit) entlang der betreffenden Größenachse (Streuung) dar. Die aus einer Stichprobe gewonnenen Kennzahlen lassen dann Rückschlüsse auf die Grundgesamtheit zu.
Dispersionsmaße: Bezüglich der Streubereiche stellt man die Häufigkeitsverteilung der Messwerte einer Gruppe von Beobachtungen (einer repräsentativen Stichprobe. sample - Teil der Grundgesamtheit) entlang der betreffenden Größenachse (Streuung) dar. Die aus einer Stichprobe gewonnenen Kennzahlen lassen dann Rückschlüsse auf die Grundgesamtheit zu.
 Die Standardabweichung sagt aus, wie stark in einem Kollektiv mit normalverteilten Daten die Werte einzelner Beobachtungen um den Mittelwert streuen. Dabei haben Ausreißer nur eine geringe Auswirkung auf den SD-Bereich.
Die Standardabweichung sagt aus, wie stark in einem Kollektiv mit normalverteilten Daten die Werte einzelner Beobachtungen um den Mittelwert streuen. Dabei haben Ausreißer nur eine geringe Auswirkung auf den SD-Bereich.  68,2% der Gesamtheit der Beobachtungen im Bereich ±1 SD um den Mittelwert,
68,2% der Gesamtheit der Beobachtungen im Bereich ±1 SD um den Mittelwert, 95,4% der Gesamtheit der Beobachtungen im Bereich ±2 SD um den Mittelwert,
95,4% der Gesamtheit der Beobachtungen im Bereich ±2 SD um den Mittelwert, 99,7% der Gesamtheit der Beobachtungen im Bereich ±3 SD um den Mittelwert
99,7% der Gesamtheit der Beobachtungen im Bereich ±3 SD um den Mittelwert vgl. unten).
vgl. unten).| CV = SD / µ |

 Abbildung: Box and whisker plot
Abbildung: Box and whisker plot
 Die Strecke zwischen der 25. und 75. Perzentile heißt Quartilsabstand (interquartile range) und
enthält die Hälfte
aller Beobachtungen - also den Bereich mit den mittleren 50% der Werte,
die im Sample ermittelt wurden. Dieser Wert ist leicht zu ermitteln und
wird von Ausreissern so gut wie nicht beeinflusst.
Die Strecke zwischen der 25. und 75. Perzentile heißt Quartilsabstand (interquartile range) und
enthält die Hälfte
aller Beobachtungen - also den Bereich mit den mittleren 50% der Werte,
die im Sample ermittelt wurden. Dieser Wert ist leicht zu ermitteln und
wird von Ausreissern so gut wie nicht beeinflusst. Vieles in der Medizin wird in Prozent (Hundertstel) angegeben. Dabei ist es wesentlich, immer die Frage zu stellen, % wovon (100% = 1), d.h. die Gesamtheit von etwas - dieses Etwas muss definiert werden.
Vieles in der Medizin wird in Prozent (Hundertstel) angegeben. Dabei ist es wesentlich, immer die Frage zu stellen, % wovon (100% = 1), d.h. die Gesamtheit von etwas - dieses Etwas muss definiert werden. Eine Prozentzahl ohne Kenntnis / Angabe der Gesamtheit (=1) ist sinnlos
Eine Prozentzahl ohne Kenntnis / Angabe der Gesamtheit (=1) ist sinnlos
 Zum Begriff der "Genauigkeit" ist zu unterscheiden zwischen
Zum Begriff der "Genauigkeit" ist zu unterscheiden zwischen  Absolutgenauigkeit (accuracy): Sie sagt aus, wie nahe der Durchschnittswert am wahren Wert liegt - d.h. wie richtig das durchschnittliche Resultat des Messverfahrens ist.
Statistisch ist dies beschreibbar als die Differenz zwischen dem
"Referenzwert" (wahren Wert) und dem Mittelwert der Messergebnisse;
Absolutgenauigkeit (accuracy): Sie sagt aus, wie nahe der Durchschnittswert am wahren Wert liegt - d.h. wie richtig das durchschnittliche Resultat des Messverfahrens ist.
Statistisch ist dies beschreibbar als die Differenz zwischen dem
"Referenzwert" (wahren Wert) und dem Mittelwert der Messergebnisse; Präzision (precision): Sie sagt aus, wie gering die Streuung ist -
d.h. wie verlässlich das Resultat bei wiederholter Messung wiederkehrt
(statistisch beschreibbar, z.B. als Normalverteilung wie in der
Abbildung). Die Präzision ist über eine Verteilungsbeschreibung
quantifizierbar (z.B. wie groß ist die Standardabweichung einer
Normalverteilung der Messergebnisse)?
Präzision (precision): Sie sagt aus, wie gering die Streuung ist -
d.h. wie verlässlich das Resultat bei wiederholter Messung wiederkehrt
(statistisch beschreibbar, z.B. als Normalverteilung wie in der
Abbildung). Die Präzision ist über eine Verteilungsbeschreibung
quantifizierbar (z.B. wie groß ist die Standardabweichung einer
Normalverteilung der Messergebnisse)?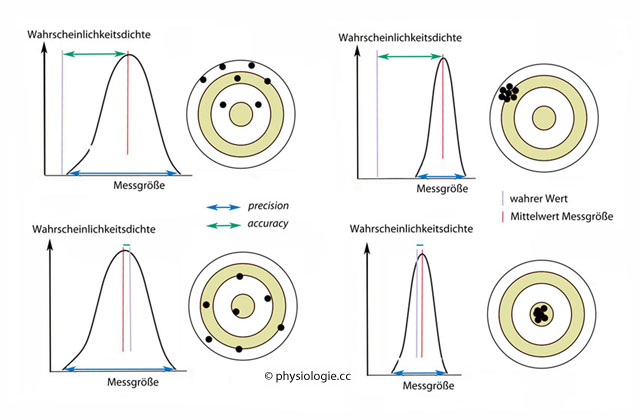
 Abbildung: Absolutgenauigkeit und Präzision
Abbildung: Absolutgenauigkeit und Präzision
 So
kann eine Waage immer wieder einen falschen Absolutwert angeben; dann
ist die Präzision möglicherweise hoch ("immer genau daneben"), die Absolutgenauigkeit aber
gering (Abweichung vom wahren Wert).
So
kann eine Waage immer wieder einen falschen Absolutwert angeben; dann
ist die Präzision möglicherweise hoch ("immer genau daneben"), die Absolutgenauigkeit aber
gering (Abweichung vom wahren Wert). Sie
kann aber auch umgekehrt im Schnitt den wahren Wert anzeigen, nur die
Einzelmessungen streuen stark - breite Verteilung; hohe
Absolutgenauigkeit, geringe Präzision; wiederholte Messungen ergeben im Schnitt das richtige Resultat.
Sie
kann aber auch umgekehrt im Schnitt den wahren Wert anzeigen, nur die
Einzelmessungen streuen stark - breite Verteilung; hohe
Absolutgenauigkeit, geringe Präzision; wiederholte Messungen ergeben im Schnitt das richtige Resultat.
 Abbildung).
Abbildung).  Als Referenzbereich bezeichnet
man einen definierten Bereich um einen Mittelwert (MW), in dem ein
dementsprechend großer Anteil aller Messwerte liegt. Legt man z.B. die
Spanne der doppelten Standardabweichung (2 SD) um den Mittelwert (MW -2
SD bis MW + 2 SD) fest, liegen ~95% der Beobachtungen in diesem
Referenzbereich. Jeweils ~2,5% der Beobachtungen fallen dann aus dem Referenzbereich
heraus, sie liegen vom Mittelwert weiter als zwei Standardabweichungen entfernt (violette Bereiche in der
Als Referenzbereich bezeichnet
man einen definierten Bereich um einen Mittelwert (MW), in dem ein
dementsprechend großer Anteil aller Messwerte liegt. Legt man z.B. die
Spanne der doppelten Standardabweichung (2 SD) um den Mittelwert (MW -2
SD bis MW + 2 SD) fest, liegen ~95% der Beobachtungen in diesem
Referenzbereich. Jeweils ~2,5% der Beobachtungen fallen dann aus dem Referenzbereich
heraus, sie liegen vom Mittelwert weiter als zwei Standardabweichungen entfernt (violette Bereiche in der  Abbildung).
Abbildung).  Liegt ein Ergenis außerhalb des
Referenzbereichs (Wahrscheinlichzkeit 5%), bedeutet das nicht
automatisch, dass z.B. ein Patient - von dem der Befund stammt - als
klinisch krank einzustufen ist; es bedeutet lediglich, dass das
Ergebnis statistisch in einem 5%-Wahrscheinlichkeitsbereich liegt (der
Patien kann vollkommen gesund sein). Zahlreiche Faktoren können einen Einfluss auf das Ergebnis haben (Probengewinnung,
Messmethode, Alter und Geschlecht der Probanden etc). Messergebnisse
sind Indikatoren, die Hinweise, aber keine 100%-ige diagnostische
Sicherheit geben.
Liegt ein Ergenis außerhalb des
Referenzbereichs (Wahrscheinlichzkeit 5%), bedeutet das nicht
automatisch, dass z.B. ein Patient - von dem der Befund stammt - als
klinisch krank einzustufen ist; es bedeutet lediglich, dass das
Ergebnis statistisch in einem 5%-Wahrscheinlichkeitsbereich liegt (der
Patien kann vollkommen gesund sein). Zahlreiche Faktoren können einen Einfluss auf das Ergebnis haben (Probengewinnung,
Messmethode, Alter und Geschlecht der Probanden etc). Messergebnisse
sind Indikatoren, die Hinweise, aber keine 100%-ige diagnostische
Sicherheit geben. Das Konfidenzintervall (confidence interval) gibt an, in welchem Bereich der Mittelwert der gesamten Population liegt, auf die man sich bezieht.
Das Konfidenzintervall (confidence interval) gibt an, in welchem Bereich der Mittelwert der gesamten Population liegt, auf die man sich bezieht.  Übersichtsgraphik: Klinisch-chemische Normbereiche
Übersichtsgraphik: Klinisch-chemische Normbereiche Physiologische ("unauffällige") Messwertbereiche bedeuten nicht immer die
doppelte Standardabweichung um den Mittelwert. Richtwertgrenzen
orientieren sich oft an klinischer Erfahrung, sie können im Rahmen von Consensus-Konferenzen festgelegt werden.
Physiologische ("unauffällige") Messwertbereiche bedeuten nicht immer die
doppelte Standardabweichung um den Mittelwert. Richtwertgrenzen
orientieren sich oft an klinischer Erfahrung, sie können im Rahmen von Consensus-Konferenzen festgelegt werden. 
 Für klinische Laborwerte wurde in dieser Website als primäre Datenquelle das Lexikon der Medizinischen Laboratoriumsdiagnostik (Gressner / Arndt, 2. Aufl. 2013, Springer-Verlag) herangezogen.
Für klinische Laborwerte wurde in dieser Website als primäre Datenquelle das Lexikon der Medizinischen Laboratoriumsdiagnostik (Gressner / Arndt, 2. Aufl. 2013, Springer-Verlag) herangezogen. Biometrische Testverfahren sollen Hypothesen
Biometrische Testverfahren sollen Hypothesen
 (vermutete Sachverhalte) anhand von Versuchsergebnissen überprüfen und gegenüber
möglicherweise irreleitenden Zufallseffekten absichern. Man erhebt Daten (durch Messung / Beobachtung gewonnene Werte oder Befunde) an Zufallsstichproben (random samples), das sind Teile des gesamten Kollektivs (an Datenträgern), die mit Hilfe spezieller Auswahlverfahren zur Datenerhebung ausgesucht werden. Die statistische Auswertung von Zufallsstichproben ist ein heuristisches Verfahren (Heuristik
(vermutete Sachverhalte) anhand von Versuchsergebnissen überprüfen und gegenüber
möglicherweise irreleitenden Zufallseffekten absichern. Man erhebt Daten (durch Messung / Beobachtung gewonnene Werte oder Befunde) an Zufallsstichproben (random samples), das sind Teile des gesamten Kollektivs (an Datenträgern), die mit Hilfe spezieller Auswahlverfahren zur Datenerhebung ausgesucht werden. Die statistische Auswertung von Zufallsstichproben ist ein heuristisches Verfahren (Heuristik ist die Methode, mit begrenztem Wissen bzw. unvollständigen Informationen zu wahrscheinlichen Aussagen zu gelangen).
ist die Methode, mit begrenztem Wissen bzw. unvollständigen Informationen zu wahrscheinlichen Aussagen zu gelangen). In
komplexen Systemen (wie meistens im medizinischen Bereich) interagieren
zahlreiche Größen, klare Ursachen-Wirkungs-Beziehungen sind oft schwer erkennbar, die Reduktion auf nur eine Einflussvariable
unmöglich. Prinzipien der
Statistik, der physiologische Gesamtzusammenhang, und individuelle
Komponenten müssen in jedem Einzelfall Berücksichtigung finden.
In
komplexen Systemen (wie meistens im medizinischen Bereich) interagieren
zahlreiche Größen, klare Ursachen-Wirkungs-Beziehungen sind oft schwer erkennbar, die Reduktion auf nur eine Einflussvariable
unmöglich. Prinzipien der
Statistik, der physiologische Gesamtzusammenhang, und individuelle
Komponenten müssen in jedem Einzelfall Berücksichtigung finden.
 bauen
auf Hypothesen auf; auch sie sind spekulativ, aber allgemeiner
gehalten als (die ihnen zugrundeliegenden) Hypothesen, die (jede für
sich) wissenschaftlich getestet werden können. Es gibt mehrere
Möglichkeiten, den Begriff "Theorie" zu definieren; in den
Naturwissenschaften versteht man darunter eine Form des rationalen
Umgangs mit Phänomenen, die in der Natur zu beobachten oder zu
erschließen sind, wobei naturwissenschaftliche Methoden und Verfahren
angewendet werden (empirische Bestätigung getroffener Annahmen,
prädiktive Potenz der Theorie etc.).
bauen
auf Hypothesen auf; auch sie sind spekulativ, aber allgemeiner
gehalten als (die ihnen zugrundeliegenden) Hypothesen, die (jede für
sich) wissenschaftlich getestet werden können. Es gibt mehrere
Möglichkeiten, den Begriff "Theorie" zu definieren; in den
Naturwissenschaften versteht man darunter eine Form des rationalen
Umgangs mit Phänomenen, die in der Natur zu beobachten oder zu
erschließen sind, wobei naturwissenschaftliche Methoden und Verfahren
angewendet werden (empirische Bestätigung getroffener Annahmen,
prädiktive Potenz der Theorie etc.). Resultat
eines statistischen Schlusses ist nicht Gewissheit (Sicherheit), sondern eine bestimmte Wahrscheinlichkeit (probability),
mit der z.B. ein Unterschied zwischen den geprüften Stichproben
(z.B. je 20 Patienten) in Bezug auf die geprüfte Einflussgröße tatsächlich besteht. Eine getroffene
Aussage (z.B. ob Kopfschmerz nach Gabe von Aspirin rascher
abklingt als bei Verwendung eines Placebo) wird als mehr oder weniger wahrscheinlich gewertet.
Resultat
eines statistischen Schlusses ist nicht Gewissheit (Sicherheit), sondern eine bestimmte Wahrscheinlichkeit (probability),
mit der z.B. ein Unterschied zwischen den geprüften Stichproben
(z.B. je 20 Patienten) in Bezug auf die geprüfte Einflussgröße tatsächlich besteht. Eine getroffene
Aussage (z.B. ob Kopfschmerz nach Gabe von Aspirin rascher
abklingt als bei Verwendung eines Placebo) wird als mehr oder weniger wahrscheinlich gewertet. 
 Abbildung: Zustands-Zeitverlauf - natürlich, mit Placebo, mit Verum (hypothetisch, vereinfacht)
Abbildung: Zustands-Zeitverlauf - natürlich, mit Placebo, mit Verum (hypothetisch, vereinfacht)
 Immer
bleibt in solchen Fällen eine
Restwahrscheinlichkeit, dass eine getroffene Schlussfolgerung (z.B. ein
getestetes Medikament reduziert Schmerzen in Dauer oder Intensität)
unzutreffend ist.
(Dabei ist es durchaus möglich, dass nicht das Medikament an sich,
sondern seine Einnahme einen schmerzlindernden Effekt hat - Placebo-Wirkung).
Immer
bleibt in solchen Fällen eine
Restwahrscheinlichkeit, dass eine getroffene Schlussfolgerung (z.B. ein
getestetes Medikament reduziert Schmerzen in Dauer oder Intensität)
unzutreffend ist.
(Dabei ist es durchaus möglich, dass nicht das Medikament an sich,
sondern seine Einnahme einen schmerzlindernden Effekt hat - Placebo-Wirkung). Was ist der p-Wert? "p" kommt von probability, es handelt sich also um ein Wahrscheinlchkeitsmaß
- ein sehr wichtiges Konzept (Wahrscheinlichkeitstheorie = Stochastik
Was ist der p-Wert? "p" kommt von probability, es handelt sich also um ein Wahrscheinlchkeitsmaß
- ein sehr wichtiges Konzept (Wahrscheinlichkeitstheorie = Stochastik  ). Der p-Wert gibt an, mit welcher
Wahrscheinlichkeit ein beobachteter Unterschied zwischen zwei
verglichenen Kollektiven nur zufällig aufgetreten ist (Sicherheit:
p=1,0; Unmöglichkeit: p=0,0).
). Der p-Wert gibt an, mit welcher
Wahrscheinlichkeit ein beobachteter Unterschied zwischen zwei
verglichenen Kollektiven nur zufällig aufgetreten ist (Sicherheit:
p=1,0; Unmöglichkeit: p=0,0).  betrachtet (Beispiel: man vermutet, Aspirin ist wirkungsvoller als
Placebo).
betrachtet (Beispiel: man vermutet, Aspirin ist wirkungsvoller als
Placebo).  Eine (allenfalls zu falsifizierende) Nullhypothese
(null hypothesis) ist die Vermutung, dass zwischen zwei zu
vergleichenden Stichproben (=Teile der Gesamtheit; dies könnten z.B. alle Kopfschmerzpatienten auf der Welt sein) kein
Unterschied (z.B. bezüglich der Kopfschmerzdauer) besteht. Die
Wahrscheinlichkeit, dass diese Vermutung zutrifft, ist umso kleiner,
je wahrscheinlicher ein Unterschied - in Bezug auf die getestete Variable - zwischen den beiden Stichproben (z.B. Aspirin vs. Placebo
Eine (allenfalls zu falsifizierende) Nullhypothese
(null hypothesis) ist die Vermutung, dass zwischen zwei zu
vergleichenden Stichproben (=Teile der Gesamtheit; dies könnten z.B. alle Kopfschmerzpatienten auf der Welt sein) kein
Unterschied (z.B. bezüglich der Kopfschmerzdauer) besteht. Die
Wahrscheinlichkeit, dass diese Vermutung zutrifft, ist umso kleiner,
je wahrscheinlicher ein Unterschied - in Bezug auf die getestete Variable - zwischen den beiden Stichproben (z.B. Aspirin vs. Placebo  ) ist.
) ist.  Relevanz: Ob der Effekt auch relevant
ist, muss unabhängig davon entschieden
werden; da kommt es auf den Zusammenhang an. Es ist möglich, dass ein signifikantes Ergebnis dennoch
irrelevant ist, z.B. weil der Effekt zu gering ausfällt - z.B. eine
Blutdrucksenkung um 1% - oder weil die Frage der Untersuchung falsch gestellt wurde.
Relevanz: Ob der Effekt auch relevant
ist, muss unabhängig davon entschieden
werden; da kommt es auf den Zusammenhang an. Es ist möglich, dass ein signifikantes Ergebnis dennoch
irrelevant ist, z.B. weil der Effekt zu gering ausfällt - z.B. eine
Blutdrucksenkung um 1% - oder weil die Frage der Untersuchung falsch gestellt wurde.

 Abbildung: Überschneidung der Verteilungskurven der Ausprägung eines Merkmals in zwei Populationen
Abbildung: Überschneidung der Verteilungskurven der Ausprägung eines Merkmals in zwei Populationen
 Fehler 1. Art
Fehler 1. Art 
 Man sagt auch, die Entscheidung
ist bei Vorliegen eines α-Fehlers falsch positiv.
Auf eine medizinische Diagnose
Man sagt auch, die Entscheidung
ist bei Vorliegen eines α-Fehlers falsch positiv.
Auf eine medizinische Diagnose  bezogen, heißt das: man geht
von einem positiven Befund aus (Vermutung: Person krank), obwohl
dies unzutreffend ist.
bezogen, heißt das: man geht
von einem positiven Befund aus (Vermutung: Person krank), obwohl
dies unzutreffend ist.  Eine diagnostische Methode mit hohem α-Risiko legt häufig ein verdächtiges Ergebnis nahe, obwohl dies nicht zutrifft ("Fehlalarm"). Oder: Ein Prüfer mit hohem α-Risiko ist besonders streng; dann werden auch zahlreiche gut vorbereitete Kandidaten negativ
beurteilt.
Eine diagnostische Methode mit hohem α-Risiko legt häufig ein verdächtiges Ergebnis nahe, obwohl dies nicht zutrifft ("Fehlalarm"). Oder: Ein Prüfer mit hohem α-Risiko ist besonders streng; dann werden auch zahlreiche gut vorbereitete Kandidaten negativ
beurteilt. Tests mit hoher Spezifität haben einen
geringen Fehler 1. Art.
Tests mit hoher Spezifität haben einen
geringen Fehler 1. Art. Fehler 2. Art
Fehler 2. Art 
 Man sagt auch, die Entscheidung ist bei Unterlaufen eines β-Fehlers falsch negativ. Auf eine medizinische
Diagnose bezogen, heißt das: die diagnostische Methode findet
nichts (klinischer Jargon: 'ohne Befund' - o.B.), obwohl die Person
objektiv krank ist.
Man sagt auch, die Entscheidung ist bei Unterlaufen eines β-Fehlers falsch negativ. Auf eine medizinische
Diagnose bezogen, heißt das: die diagnostische Methode findet
nichts (klinischer Jargon: 'ohne Befund' - o.B.), obwohl die Person
objektiv krank ist.  Eine Methode mit
hohem β-Risiko ist diagnostisch unempfindlich. Oder: Ein Prüfer mit hohem β-Risiko, d.h. geringer test power (=1-ß), ist
besonders mild ("Laissez-faire"-Typ); bei ihm kommen auch ungenügend vorbereitete Kandidaten
durch (was angenehm für Medizinstudent/inn/en, aber schlecht für deren zukünftige Patienten ist).
Eine Methode mit
hohem β-Risiko ist diagnostisch unempfindlich. Oder: Ein Prüfer mit hohem β-Risiko, d.h. geringer test power (=1-ß), ist
besonders mild ("Laissez-faire"-Typ); bei ihm kommen auch ungenügend vorbereitete Kandidaten
durch (was angenehm für Medizinstudent/inn/en, aber schlecht für deren zukünftige Patienten ist). Tests mit hoher Sensitivität haben einen
geringen Fehler 2. Art.
Tests mit hoher Sensitivität haben einen
geringen Fehler 2. Art. Die Prüfungssituation ist nur ein Spezialfall der Unsicherheit, die generell auftritt,
wenn sich ein (vermuteter) Sachverhalt nicht direkt, sondern nur auf
dem Weg einer (eingeschränkt die "Wahrheit" abbildenden) Messmethode
offenbaren kann. Keine
Bestimmungsmethode bietet absolut 'richtige' Resultate zur Frage, wie
sicher eine Annahme über einen Sachverhalt tatsächlich zutrifft - über
die Fachkenntnisse eines Prüfungskandidaten, einen
Funktionsmechanismus, eine medizinische Diagnose, den
Gesundheitszustand einer Person oder anderes. Es verbleibt immer eine
Unsicherheit - z.B. kann eine Blutprobe falsch entnommen, bearbeitet,
gelagert, transportiert, umgefüllt, zugeordnet oder gemessen worden
sein, ohne dass dies aufgefallen wäre. (Der physiologische Gesamtzusammenhang
sowie individuelle Komponenten - Geschlecht, Alter, Genetik, Umwelt etc
- spielen ebenfalls eine Rolle und müssen in jedem Einzelfall
Berücksichtigung finden.)
Die Prüfungssituation ist nur ein Spezialfall der Unsicherheit, die generell auftritt,
wenn sich ein (vermuteter) Sachverhalt nicht direkt, sondern nur auf
dem Weg einer (eingeschränkt die "Wahrheit" abbildenden) Messmethode
offenbaren kann. Keine
Bestimmungsmethode bietet absolut 'richtige' Resultate zur Frage, wie
sicher eine Annahme über einen Sachverhalt tatsächlich zutrifft - über
die Fachkenntnisse eines Prüfungskandidaten, einen
Funktionsmechanismus, eine medizinische Diagnose, den
Gesundheitszustand einer Person oder anderes. Es verbleibt immer eine
Unsicherheit - z.B. kann eine Blutprobe falsch entnommen, bearbeitet,
gelagert, transportiert, umgefüllt, zugeordnet oder gemessen worden
sein, ohne dass dies aufgefallen wäre. (Der physiologische Gesamtzusammenhang
sowie individuelle Komponenten - Geschlecht, Alter, Genetik, Umwelt etc
- spielen ebenfalls eine Rolle und müssen in jedem Einzelfall
Berücksichtigung finden.) Was wir über einen Sachverhalt schon wissen (prior knowledge) und eine entsprechende pretest probability ergibt, und
Was wir über einen Sachverhalt schon wissen (prior knowledge) und eine entsprechende pretest probability ergibt, und neue Beobachtungen (z.B. Laborbefund), die dieses Wissen beeinflussen und die posttest probability verändern (erhöhen oder senken).
neue Beobachtungen (z.B. Laborbefund), die dieses Wissen beeinflussen und die posttest probability verändern (erhöhen oder senken).
 Abbildung: 4-Felder-Matrix zu Testergebnissen: Beurteilung eines Klassifikators (dieser ordnet zu einem von zwei Kategorien zu)
Abbildung: 4-Felder-Matrix zu Testergebnissen: Beurteilung eines Klassifikators (dieser ordnet zu einem von zwei Kategorien zu) f = falsch
f = falsch  p = positiv
p = positiv  n = negativ
n = negativ
 Es geht also um
den erwarteten Nutzen diagnostischer Tests.
Dabei ist zu beachten, dass die diagnostische Aussage
nie 'sicher', sondern nur wahrscheinlich sein kann. Die hier
besprochenen Konzepte der Sensitivität, Spezifität und des prädiktiven
Wertes sind auf Tests (wissenschaftlich, labormedizinisch etc)
anwendbar, die eine Ja-Nein-Antwort auf die Frage geben, ob ein
bestimmter Zustand (z.B. eine Erkrankung) vorliegt oder nicht.
Es geht also um
den erwarteten Nutzen diagnostischer Tests.
Dabei ist zu beachten, dass die diagnostische Aussage
nie 'sicher', sondern nur wahrscheinlich sein kann. Die hier
besprochenen Konzepte der Sensitivität, Spezifität und des prädiktiven
Wertes sind auf Tests (wissenschaftlich, labormedizinisch etc)
anwendbar, die eine Ja-Nein-Antwort auf die Frage geben, ob ein
bestimmter Zustand (z.B. eine Erkrankung) vorliegt oder nicht.  Liegt
|LR] unter 1, hat sich die Wahrscheinlichkeit für das Vorliegen der
Erkrankung erniedrigt; die entsprechende LR- berechnet sich aus
Liegt
|LR] unter 1, hat sich die Wahrscheinlichkeit für das Vorliegen der
Erkrankung erniedrigt; die entsprechende LR- berechnet sich aus Liegt
|LR] über 1, hat sich die Wahrscheinlichkeit für das Vorliegen der
Erkrankung erhöht; die entsprechende LR+ berechnet sich aus
Liegt
|LR] über 1, hat sich die Wahrscheinlichkeit für das Vorliegen der
Erkrankung erhöht; die entsprechende LR+ berechnet sich aus Ermittelte Messwerte (in Blut, Serum, Harn u.a.) werden danach beurteilt, ob sie in einem festgesetzten Referenzbereich
liegen und damit diagnostisch unverdächtig sind. Liegen sie außerhalb
dieses Bereichs, kann dennoch ein Fehler 1. Art vorliegen (gesunder
Mensch mit "verdächtigem" Laborbefund). Umgekehrt garantiert ein Wert
innerhalb des Bereichs nicht, dass keine Krankheit vorliegt (es kann
ein Fehler 2. Art vorliegen); beides kann jeweils nur mit einer
bestimmten Wahrscheinlichkeit angenommen werden.
Ermittelte Messwerte (in Blut, Serum, Harn u.a.) werden danach beurteilt, ob sie in einem festgesetzten Referenzbereich
liegen und damit diagnostisch unverdächtig sind. Liegen sie außerhalb
dieses Bereichs, kann dennoch ein Fehler 1. Art vorliegen (gesunder
Mensch mit "verdächtigem" Laborbefund). Umgekehrt garantiert ein Wert
innerhalb des Bereichs nicht, dass keine Krankheit vorliegt (es kann
ein Fehler 2. Art vorliegen); beides kann jeweils nur mit einer
bestimmten Wahrscheinlichkeit angenommen werden. Dies erreicht man durch Randomisierung,
Dies erreicht man durch Randomisierung,  d.h. zufällige Zuordnung von Probanden zu den Testgruppen, um
(unbeabsichtigte) systematische Fehler (Trend, bias) zu
vermeiden - solche Fehler täuschen sonst einen Effekt vor, der
in Realität nicht besteht. Dies ist eine Anforderung an das Studiendesign.
d.h. zufällige Zuordnung von Probanden zu den Testgruppen, um
(unbeabsichtigte) systematische Fehler (Trend, bias) zu
vermeiden - solche Fehler täuschen sonst einen Effekt vor, der
in Realität nicht besteht. Dies ist eine Anforderung an das Studiendesign.  verteilungsabhängige (parametrische) statistische Verfahren (parametric tests), z.B. der t-Test (Student's t), der zwei, und
die ANOVA (analysis of variance), die zwei oder mehr normalverteilte Stichproben (Gauss-Glockenkurve, s. oben) vergleichen lässt;
verteilungsabhängige (parametrische) statistische Verfahren (parametric tests), z.B. der t-Test (Student's t), der zwei, und
die ANOVA (analysis of variance), die zwei oder mehr normalverteilte Stichproben (Gauss-Glockenkurve, s. oben) vergleichen lässt; verteilungsunabhängige (parameterfreie) Verfahren (non-parametric tests), z.B. der Mann-Whitney U-, Wilcoxon-, Kruskal-Wallis- oder Friedman-Test: Nicht die gemessenen Werte an sich werden verglichen, sondern aufgrund
dieser Werte ermittelte Rangzahlen
(Beispiel Altersverteilung: Statt dem Alter in Jahren - z.B. 9 bis 90
Jahre - werden die Ränge der Datenpunkte (1 bis x) verglichen). Diese
Verfahren werden genutzt, wenn die Werte der Stichproben nicht normalverteilt sind.
verteilungsunabhängige (parameterfreie) Verfahren (non-parametric tests), z.B. der Mann-Whitney U-, Wilcoxon-, Kruskal-Wallis- oder Friedman-Test: Nicht die gemessenen Werte an sich werden verglichen, sondern aufgrund
dieser Werte ermittelte Rangzahlen
(Beispiel Altersverteilung: Statt dem Alter in Jahren - z.B. 9 bis 90
Jahre - werden die Ränge der Datenpunkte (1 bis x) verglichen). Diese
Verfahren werden genutzt, wenn die Werte der Stichproben nicht normalverteilt sind.  Vergleicht man asymmetrisch verteilte Stichproben, sollte man nicht-parametrische Tests zur Hypothesenverifizierung einsetzen.
Vergleicht man asymmetrisch verteilte Stichproben, sollte man nicht-parametrische Tests zur Hypothesenverifizierung einsetzen.| S = (µ - M) / SD |
 Es ist legitim, Daten so umzuwandeln, dass aus einer schiefen Verteilung
eine normalverteilte wird, z.B. durch Logarithmierung. Dann können (auch)
parametrische Tests zur Anwendung kommen.
Es ist legitim, Daten so umzuwandeln, dass aus einer schiefen Verteilung
eine normalverteilte wird, z.B. durch Logarithmierung. Dann können (auch)
parametrische Tests zur Anwendung kommen. Bedeutung s. oben), der bei allen diesen Tests ermittelt werden kann.
Bedeutung s. oben), der bei allen diesen Tests ermittelt werden kann. Der Chi-Quadrat- (chi-squared) Test: Dieser vergleicht den Unterschied zwischen beobachteter und erwarteter (Nullhypothese wahr) Stichprobenverteilung; je größer der Unterschied, desto größer der Χ2-Wert (bei fehlender Ungleichheit ist [Χ2]=0). Auch bei diesem Test kann man den p-Wert ermitteln, um die Wahrscheinlichkeit
anzugeben, dass in Wirklichkeit kein Unterschied zwischen den
Stichproben besteht.
Der Chi-Quadrat- (chi-squared) Test: Dieser vergleicht den Unterschied zwischen beobachteter und erwarteter (Nullhypothese wahr) Stichprobenverteilung; je größer der Unterschied, desto größer der Χ2-Wert (bei fehlender Ungleichheit ist [Χ2]=0). Auch bei diesem Test kann man den p-Wert ermitteln, um die Wahrscheinlichkeit
anzugeben, dass in Wirklichkeit kein Unterschied zwischen den
Stichproben besteht.
 Messwerte können qualitativ (z.B. männlich / weiblich) oder quantitativ
dargestellt werden, letztere diskret (z.B. Leukozytenzahl) oder stetig
(z.B. Betrag des Blutdrucks). Die Art der Darstellung einer Häufigkeitsverteilung sowie passende statistische Verfahren hängen
von der Art des Merkmals und seiner Verteilung ab. Biometrie wendet statistische Methoden auf
die Lösung biologischer Probleme an. Man unterscheidet deskriptive
(Mittelwert, Varianz) und induktive Statistik (Hypothesenverifizierung, Wahrscheinlichkeitsrechnung) Messwerte können qualitativ (z.B. männlich / weiblich) oder quantitativ
dargestellt werden, letztere diskret (z.B. Leukozytenzahl) oder stetig
(z.B. Betrag des Blutdrucks). Die Art der Darstellung einer Häufigkeitsverteilung sowie passende statistische Verfahren hängen
von der Art des Merkmals und seiner Verteilung ab. Biometrie wendet statistische Methoden auf
die Lösung biologischer Probleme an. Man unterscheidet deskriptive
(Mittelwert, Varianz) und induktive Statistik (Hypothesenverifizierung, Wahrscheinlichkeitsrechnung)  Deskriptive
Statistik ermittelt Häufigkeitsverteilungen und gibt
Streumaße an, wie den arithmetrischen Mittelwert (AMW), den Modalwert oder den
Medianwert. Der AMW liegt
beim häufigsten Wert einer Normalverteilung (Gauss-sche Glockenkurve), die
Standardabweichung (SD) kennzeichnet die Streuung der Messwerte um den
Mittelwert: Der Bereich AMW ± 1 SD umfasst 68,2%; AMW ± 2 SD 95,4%; und
AMW ± 3 SD 99,7% aller Beobachtungen. Bei einer perfekten symmetrischen Verteilung haben Modal-, Median- und Mittelwert den identischen Betrag. Teilt der AMW die Verteilung nicht in zwei gleich
große Hälften, liegt keine Normalverteilung vor; der
Medianwert trennt die oberen von den unteren 50% der Verteilung, der Modalwert ist der häufigste Wert in der Stichprobe.
Box and whisker-Plots zeigen die
25- und 75%-Perzentile (box), definierte Minimal- und Maximalwerte
(whiskers) und (individuell) außerhalb liegende Ausreißer Deskriptive
Statistik ermittelt Häufigkeitsverteilungen und gibt
Streumaße an, wie den arithmetrischen Mittelwert (AMW), den Modalwert oder den
Medianwert. Der AMW liegt
beim häufigsten Wert einer Normalverteilung (Gauss-sche Glockenkurve), die
Standardabweichung (SD) kennzeichnet die Streuung der Messwerte um den
Mittelwert: Der Bereich AMW ± 1 SD umfasst 68,2%; AMW ± 2 SD 95,4%; und
AMW ± 3 SD 99,7% aller Beobachtungen. Bei einer perfekten symmetrischen Verteilung haben Modal-, Median- und Mittelwert den identischen Betrag. Teilt der AMW die Verteilung nicht in zwei gleich
große Hälften, liegt keine Normalverteilung vor; der
Medianwert trennt die oberen von den unteren 50% der Verteilung, der Modalwert ist der häufigste Wert in der Stichprobe.
Box and whisker-Plots zeigen die
25- und 75%-Perzentile (box), definierte Minimal- und Maximalwerte
(whiskers) und (individuell) außerhalb liegende Ausreißer Absolutgenauigkeit
(accuracy) gibt die Richtigkeit einer Messung als die Differenz
zwischen dem wahren Wert und dem Mittelwert der Messergebnisse an,
Präzision (precision) die Wiederkehrgenauigkeit als Verteilungsbreite
(schmale Streuung → hohe Präzision). Das
Konfidenzintervall gibt an, in welchem Bereich der wirkliche Mittelwert
(derjenige der gesamten Population) liegt Absolutgenauigkeit
(accuracy) gibt die Richtigkeit einer Messung als die Differenz
zwischen dem wahren Wert und dem Mittelwert der Messergebnisse an,
Präzision (precision) die Wiederkehrgenauigkeit als Verteilungsbreite
(schmale Streuung → hohe Präzision). Das
Konfidenzintervall gibt an, in welchem Bereich der wirkliche Mittelwert
(derjenige der gesamten Population) liegt Schließende
Statistik errechnet, wie wahrscheinlich vermutete Sachverhalte
zutreffen (Hypothesenverifizierung). Dazu erhebt man Daten an
Zufallsstichproben, die mittels Auswahlverfahren ausgesucht werden. Der p-Wert quantifiziert die Wahrscheinlichkeit der Nullhypothese, d.h. dass sich die verglichenen Kollektive hinsichtlich des untersuchten Merkmals nicht
unterscheiden (Sicherheit: p=1,0; Unmöglichkeit: p=0,0). Liegt er z.B.
bei 0,05, heißt das, dass der Effekt in einem von 20 Untersuchungen
(5%) durch Zufall auftreten würde, üblicherweise gilt das Ergebnis dann
als signifikant. Ob der Effekt auch relevant ist, hängt vom Zusammenhang ab Schließende
Statistik errechnet, wie wahrscheinlich vermutete Sachverhalte
zutreffen (Hypothesenverifizierung). Dazu erhebt man Daten an
Zufallsstichproben, die mittels Auswahlverfahren ausgesucht werden. Der p-Wert quantifiziert die Wahrscheinlichkeit der Nullhypothese, d.h. dass sich die verglichenen Kollektive hinsichtlich des untersuchten Merkmals nicht
unterscheiden (Sicherheit: p=1,0; Unmöglichkeit: p=0,0). Liegt er z.B.
bei 0,05, heißt das, dass der Effekt in einem von 20 Untersuchungen
(5%) durch Zufall auftreten würde, üblicherweise gilt das Ergebnis dann
als signifikant. Ob der Effekt auch relevant ist, hängt vom Zusammenhang ab Fehler 1. Art
(α-Fehler) heißt, die Nullhypothese wird zurückgewiesen, obwohl sie in
Wirklichkeit richtig ist (α-Risiko): Die Entscheidung ist falsch
positiv (Vermutung: Person krank, obwohl das nicht zutrifft:
"Fehlalarm"). Spezifität ist
die Wahrscheinlichkeit, mit der der Test in der Gruppe der Gesunden korrekterweise ein negatives Ergebnis anzeigt;
Tests mit hoher Spezifität haben einen geringen Fehler 1. Art Fehler 1. Art
(α-Fehler) heißt, die Nullhypothese wird zurückgewiesen, obwohl sie in
Wirklichkeit richtig ist (α-Risiko): Die Entscheidung ist falsch
positiv (Vermutung: Person krank, obwohl das nicht zutrifft:
"Fehlalarm"). Spezifität ist
die Wahrscheinlichkeit, mit der der Test in der Gruppe der Gesunden korrekterweise ein negatives Ergebnis anzeigt;
Tests mit hoher Spezifität haben einen geringen Fehler 1. Art  Fehler 2. Art (β-Fehler) bedeutet, die Nullhypothese wird beibehalten, obwohl sie in Wirklichkeit falsch ist (β-Risiko): Die Entscheidung ist falsch negativ (diagnostisch unempfindlich - "o.B.", obwohl die Person objektiv krank ist). Sensitivität
ist die Wahrscheinlichkeit, mit der der Test in der Gruppe der Kranken korrekterweise ein
positives Testergebnis anzeigt; Tests mit hoher Sensitivität haben
einen geringen Fehler 2. Art Fehler 2. Art (β-Fehler) bedeutet, die Nullhypothese wird beibehalten, obwohl sie in Wirklichkeit falsch ist (β-Risiko): Die Entscheidung ist falsch negativ (diagnostisch unempfindlich - "o.B.", obwohl die Person objektiv krank ist). Sensitivität
ist die Wahrscheinlichkeit, mit der der Test in der Gruppe der Kranken korrekterweise ein
positives Testergebnis anzeigt; Tests mit hoher Sensitivität haben
einen geringen Fehler 2. Art  Messwerte werden in erster Linie danach beurteilt, ob sie in einem
festgesetzten Referenzbereich liegen (diagnostisch unverdächtig sind).
Liegen sie innerhalb des Referenzbereichs, kann dennoch ein Fehler 2. Art vorliegen (kranker Mensch mit unverdächtigem Befund); liegt er außerhalb, kann dennoch ein Fehler 1. Art vorliegen (gesunder Mensch mit verdächtigem Befund). Eine diagnostische Aussage kann nie zu 100% sicher sein. Der prädiktive Wert ist ein Maß für die Wahrscheinlichkeit richtiger Diagnosen: Er gibt
an, wie hoch der Prozentsatz der zutreffenden (negativen oder
positiven) Befunde an der Gesamtheit der (negativen oder positiven)
Situationen ist
Messwerte werden in erster Linie danach beurteilt, ob sie in einem
festgesetzten Referenzbereich liegen (diagnostisch unverdächtig sind).
Liegen sie innerhalb des Referenzbereichs, kann dennoch ein Fehler 2. Art vorliegen (kranker Mensch mit unverdächtigem Befund); liegt er außerhalb, kann dennoch ein Fehler 1. Art vorliegen (gesunder Mensch mit verdächtigem Befund). Eine diagnostische Aussage kann nie zu 100% sicher sein. Der prädiktive Wert ist ein Maß für die Wahrscheinlichkeit richtiger Diagnosen: Er gibt
an, wie hoch der Prozentsatz der zutreffenden (negativen oder
positiven) Befunde an der Gesamtheit der (negativen oder positiven)
Situationen ist Hypothesenverifizierung braucht Randomisierung (zufallsgeleitete Zuordnung
von Probanden zu Testgruppen), um systematische Fehler (die einen nicht
existierenden Effekt vortäuschen könnten) zu vermeiden (Anforderung an
das Studiendesign). Bei Normalverteilungen (Glockenkurve) können
verteilungsabhängige (parametrische) statistische Verfahren, z.B.
Student's t-Test oder ANOVA (analysis of variance) zur Anwendung
kommen. Bei anderen - negativ (links-) oder positiv (rechtsschiefen) -
Verteilungen verwendet man verteilungsunabhängige
(parameterfreie) Verfahren, z.B. Mann-Whitney U-, Wilcoxon-,
Kruskal-Wallis- oder Friedman-Test (nicht gemessene Werte, sondern
Rangzahlen werden verglichen). Der Grad der Asymmetrie (skewness) der
Verteilung kann durch eine entsprechende Kennzahl quantifiziert werden,
beispielsweise Pearson's S. Man kann schiefe zu Normalverteilungen
umformen, z.B. durch Logarithmierung Hypothesenverifizierung braucht Randomisierung (zufallsgeleitete Zuordnung
von Probanden zu Testgruppen), um systematische Fehler (die einen nicht
existierenden Effekt vortäuschen könnten) zu vermeiden (Anforderung an
das Studiendesign). Bei Normalverteilungen (Glockenkurve) können
verteilungsabhängige (parametrische) statistische Verfahren, z.B.
Student's t-Test oder ANOVA (analysis of variance) zur Anwendung
kommen. Bei anderen - negativ (links-) oder positiv (rechtsschiefen) -
Verteilungen verwendet man verteilungsunabhängige
(parameterfreie) Verfahren, z.B. Mann-Whitney U-, Wilcoxon-,
Kruskal-Wallis- oder Friedman-Test (nicht gemessene Werte, sondern
Rangzahlen werden verglichen). Der Grad der Asymmetrie (skewness) der
Verteilung kann durch eine entsprechende Kennzahl quantifiziert werden,
beispielsweise Pearson's S. Man kann schiefe zu Normalverteilungen
umformen, z.B. durch Logarithmierung |
